Fuerza Centrífuga Y centrípeta. Aplicación de tercera derivada

Fuerza Centrípeta

Proveniente del vocablo en latín Centrípetus refiere a lo que se desplaza rumbo al centro o a lo que produce atracción hacia  la ubicación de él

Atracción hacia el centro de la curva

La Fuerza centrípeta es cuando un objeto que describe una trayectoria circular, por cuestiones de la fuerza ejercida por quien hace la acción, tiene la sensación de que es llevado al interior del centro de la circunferencia que se describe. La fuerza centrípeta actúa con atracción, sobre el cuerpo, domina el espacio cuestionado y propone las direcciones que este debe llevar. Contraria a la Fuerza centrífuga, que lo que se busca es una salida del circulo, la fuerza centrípeta involucra dos o mas fuerzas para mantener o acercar lo mas posible el objeto al centro de la esfera que se recrea.

os objetos con movimiento rectilíneo uniforme tienen una velocidad constante; pero un objeto que se mueva sobre una trayectoria circular con rapidez constante experimenta continuamente un cambio en la dirección de su movimiento, esto es, en la dirección de la velocidad. Puesto que la velocidad cambia, existe una aceleración. La magnitud de este cambio de dirección de la velocidad por unidad de tiempo es la aceleración centrípeta, representada por un vector dirigido hacia el centro de la circunferencia dado por

                                          

Donde:

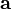 es la aceleración centrípeta.

 es el módulo de la velocidad.

 es el radio de la trayectoria circular (en general, el radio de curvatura).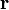

 el vector de posición.

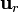 el versor radial.

 la velocidad angular.

Según la segunda ley de Newton, para que se produzca una aceleración debe actuar una fuerza en la dirección de esa aceleración. Así, si consideramos una partícula de masa  en movimiento circular uniforme, estará sometida a una fuerza centrípeta dada por:

                                         

Ejemplos en la vida cotidiana.

1. Atracción del Sol a la tierra y demás planetas.  Debido a la gran masa del sol este ejerce un fuerza gravitacional (centrípeta) sobre la tierra que la obliga a describir una trayectoria elíptica

    2. Un objeto que se hace girar amarrado a una cuerda. Al hacerlo con la suficiente fuerza, el objeto va a            estirar la cuerda de tal forma que describe una trayectoria circular, sin embargo... El cuerpo no puede seguir          su trayectoria tangencial como debería ya que la cuerda está ejerciendo una fuerza centrípeta sobre el.

                                             

  3. En un rizo de una montaña rusa. Al momento en el que los pasajeros de la montaña rusa están de cabeza van a sentir que son impulsados hacia el centro del rizo, debido a la sumatoria de pesos entre el carro y el peso de la persona, sin embargo, los cinturones de seguridad mantienen al pasajero en su sitio

 Fuerza centrífuga

La fuerza centrifuga esta basada en un eje de referencia con eje giratorio, respecto del cual, el objeto que gira a su alrededor crea una fuerza no visible hacia afuera, se supone en el estudio, que dicha partícula esta atada al eje, creando un patrón de revolución paralelo respecto de donde se origina la fuerza.

Perteneciente a la mecánica newtoniana, La Fuerza Centrifuga y si opuesta La Fuerza centrípeta son magnitudes a las que no se le aprecia la sensación desde el punto de vista de un espectador. La fuerza centrifuga, desplaza al cuerpo por inercia hacia afuera del eje ya que la gravedad y el peso permiten que ese Fenómeno ocurra, sin embargo, quien ve el desde afuera del eje el comportamiento del objeto, no percibirá la atracción de un vacío inexistente que hala al cuerpo fuera de su eje.

Ejemplos en la vida cotidiana.

1. Rotación de la tierra con respecto al sol. Así mismo como la tierra es atraída al sol por su considerable mas, la fuerza centrífuga evita que el planeta choque con la estrella 

1. La lavadora al lavar la ropa. Cuando el tambor de la lavadora internamente gira a alta velocidad ocurre que la ropa queda pegada a la pared del tambor, esta acción producida por la fuerza centrífuga

1. Al dar vueltas con agarrado  a un eje vertical ( que podría ser otra persona) el cuerpo va a sentir que está siendo atraído hacia atrás, sin embargo al soltarse se genera una trayectoria tangencial

Aplicaciones de la tercera derivada.

La tercera derivada permite indicar en caso de que la función tenga máximos o mínimos, si el valor de la incógnita es mayor que 0, el valor es un mínimo. Si en cambio, es menor que 0, el valor es un máximo.
Ahora, en general, en física muchos fenómenos se pueden describir por medio de una función escalar, denominada potencial que se extiende sobre alguna región en particular (por ejemplo el potencial gravitatorio o eléctrico) con la cual se puede asociar energía potencial a una partícula en dicha región. 
La tercera derivada de la energía potencial (segunda de la fuerza) nos indicaría sobre las regiones en las cuales la fuerza toma valores extremales (máximos o mínimos). 
Se podría saber en que regiones, afectadas por una distribución de cargas, la fuerza eléctrica sobre una carga de prueba será máxima o mínima (localmente).