Ley de los gases Ideales

Qué son gases ideales? 

Un gas ideal es un gas teórico compuesto de un conjunto de partículas puntuales con desplazamiento aleatorio que no interactúan entre sí. El concepto de gas ideal es útil porque el mismo se comporta según la ley de los gases ideales, una ecuación de estado simplificada, y que puede ser analizada mediante la mecánica estadística.

Tipos de gases ideales 

Existen tres clases básicas de gas ideal:

• El clásico o gas ideal de Maxwell-Boltzmann
• El gas ideal cuántico de Bose, compuesto de bosones
• El gas ideal cuántico de Fermi, compuesto de fermiones

Ley de Boyle

La Ley de Boyle-Mariotte (o Ley de Boyle), formulada por Robert Boyle y Edme Mariotte, es una de las leyes de los gases ideales que relaciona el volumen y la presión de una cierta cantidad de gas mantenida a temperatura constante. La ley dice que el volumen es inversamente proporcional a la presión: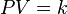 

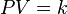
donde  es constante si la temperatura y la masa del gas permanecen constantes.

Cuando aumenta la presión, el volumen disminuye, mientras que si la presión disminuye el volumen aumenta. El valor exacto de la constante k no es necesario conocerlo para poder hacer uso de la Ley; si consideramos las dos situaciones de la figura, manteniendo constante la cantidad de gas y la temperatura, deberá cumplirse la relación

Ley de Charles

Si la cantidad de gas y la presión permanecen constantes, es razonable suponer que el volumen aumente al aumentar la temperatura. Un aumento de temperatura implica un aumento de la energía cinética media de las partículas, por tanto, un aumento de su velocidad y de la frecuencia e intensidad de los choques de éstas con las paredes. Si la pared es elástica (por ejemplo, un globo) o se puede desplazar (por ejemplo, un embolo) y la presión exterior (que iguala a la interior) permanece constante, entonces planteamos que el volumen del gas, V, debe ser proporcional a su temperatura, T  (V = K · T , para P y N constantes).

Ley de Gay-Lussac

Si la cantidad de gas y el volumen permanecen constantes, es lógico suponer que la presión aumente al aumentar la temperatura. Como hemos comentado, un aumento de temperatura implica un aumento de la velocidad de las partículas y, en consecuencia, de la frecuencia e intensidad de los choques de ellas con las paredes. Matemáticamente expresamos la segunda ley de Gay-Lussac ley diciendo que la presión, P, debe ser proporcional a la temperatura (P = k · T , para V y N constantes)

Todas ellas se condensan en la siguiente fórmula que es aplicable para una misma cantidad de gas:

Por esta razón y para n moles siendo las condiciones de presión y temperatura cualesquiera podemos poner que:

 P₁ · V₁ / T₁ = P₂ · V₂ / T₂

PV = nRT

donde:

• P es la presión
• V es el volumen
• T es la temperatura absoluta (en grados Kelvin)
• R Pertenece a un valor constante. Conocida como constante ideal de los gases

Esta es conocida como la ley general de los gases.

Fuerza Centrífuga Y centrípeta. Aplicación de tercera derivada

Fuerza Centrípeta

Proveniente del vocablo en latín Centrípetus refiere a lo que se desplaza rumbo al centro o a lo que produce atracción hacia  la ubicación de él

Atracción hacia el centro de la curva

La Fuerza centrípeta es cuando un objeto que describe una trayectoria circular, por cuestiones de la fuerza ejercida por quien hace la acción, tiene la sensación de que es llevado al interior del centro de la circunferencia que se describe. La fuerza centrípeta actúa con atracción, sobre el cuerpo, domina el espacio cuestionado y propone las direcciones que este debe llevar. Contraria a la Fuerza centrífuga, que lo que se busca es una salida del circulo, la fuerza centrípeta involucra dos o mas fuerzas para mantener o acercar lo mas posible el objeto al centro de la esfera que se recrea.

os objetos con movimiento rectilíneo uniforme tienen una velocidad constante; pero un objeto que se mueva sobre una trayectoria circular con rapidez constante experimenta continuamente un cambio en la dirección de su movimiento, esto es, en la dirección de la velocidad. Puesto que la velocidad cambia, existe una aceleración. La magnitud de este cambio de dirección de la velocidad por unidad de tiempo es la aceleración centrípeta, representada por un vector dirigido hacia el centro de la circunferencia dado por

                                          

Donde:

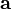 es la aceleración centrípeta.

 es el módulo de la velocidad.

 es el radio de la trayectoria circular (en general, el radio de curvatura).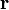

 el vector de posición.

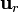 el versor radial.

 la velocidad angular.

Según la segunda ley de Newton, para que se produzca una aceleración debe actuar una fuerza en la dirección de esa aceleración. Así, si consideramos una partícula de masa  en movimiento circular uniforme, estará sometida a una fuerza centrípeta dada por:

                                         

Ejemplos en la vida cotidiana.

1. Atracción del Sol a la tierra y demás planetas.  Debido a la gran masa del sol este ejerce un fuerza gravitacional (centrípeta) sobre la tierra que la obliga a describir una trayectoria elíptica

    2. Un objeto que se hace girar amarrado a una cuerda. Al hacerlo con la suficiente fuerza, el objeto va a            estirar la cuerda de tal forma que describe una trayectoria circular, sin embargo... El cuerpo no puede seguir          su trayectoria tangencial como debería ya que la cuerda está ejerciendo una fuerza centrípeta sobre el.

                                             

  3. En un rizo de una montaña rusa. Al momento en el que los pasajeros de la montaña rusa están de cabeza van a sentir que son impulsados hacia el centro del rizo, debido a la sumatoria de pesos entre el carro y el peso de la persona, sin embargo, los cinturones de seguridad mantienen al pasajero en su sitio

 Fuerza centrífuga

La fuerza centrifuga esta basada en un eje de referencia con eje giratorio, respecto del cual, el objeto que gira a su alrededor crea una fuerza no visible hacia afuera, se supone en el estudio, que dicha partícula esta atada al eje, creando un patrón de revolución paralelo respecto de donde se origina la fuerza.

Perteneciente a la mecánica newtoniana, La Fuerza Centrifuga y si opuesta La Fuerza centrípeta son magnitudes a las que no se le aprecia la sensación desde el punto de vista de un espectador. La fuerza centrifuga, desplaza al cuerpo por inercia hacia afuera del eje ya que la gravedad y el peso permiten que ese Fenómeno ocurra, sin embargo, quien ve el desde afuera del eje el comportamiento del objeto, no percibirá la atracción de un vacío inexistente que hala al cuerpo fuera de su eje.

Ejemplos en la vida cotidiana.

1. Rotación de la tierra con respecto al sol. Así mismo como la tierra es atraída al sol por su considerable mas, la fuerza centrífuga evita que el planeta choque con la estrella 

1. La lavadora al lavar la ropa. Cuando el tambor de la lavadora internamente gira a alta velocidad ocurre que la ropa queda pegada a la pared del tambor, esta acción producida por la fuerza centrífuga

1. Al dar vueltas con agarrado  a un eje vertical ( que podría ser otra persona) el cuerpo va a sentir que está siendo atraído hacia atrás, sin embargo al soltarse se genera una trayectoria tangencial

Aplicaciones de la tercera derivada.

La tercera derivada permite indicar en caso de que la función tenga máximos o mínimos, si el valor de la incógnita es mayor que 0, el valor es un mínimo. Si en cambio, es menor que 0, el valor es un máximo.
Ahora, en general, en física muchos fenómenos se pueden describir por medio de una función escalar, denominada potencial que se extiende sobre alguna región en particular (por ejemplo el potencial gravitatorio o eléctrico) con la cual se puede asociar energía potencial a una partícula en dicha región. 
La tercera derivada de la energía potencial (segunda de la fuerza) nos indicaría sobre las regiones en las cuales la fuerza toma valores extremales (máximos o mínimos). 
Se podría saber en que regiones, afectadas por una distribución de cargas, la fuerza eléctrica sobre una carga de prueba será máxima o mínima (localmente).