Taller Matemáticas 3 by Stephanie Mosquera on Scribd
martes, 16 de agosto de 2016
martes, 2 de agosto de 2016
Función Error(erf) y Función Error Complementario(erfc)
Función Error
La función error, denotada como erf ( x) , es una función trascendental que aparece en
probabilidad, estadística, y en la solución de ecuaciones diferenciales parciales. También se le
conoce como función error de Gauss.
En matemáticas, la función error es una función especial (no elemental) que se utiliza en el campo de la probabilidad, la estadística y las ecuaciones diferenciales parciales. La función queda definida por la expresión:
La función error complementaria, llamada erfc, se define a partir de la función error:

Grafica de la función error Función Error Complementaria
Erfc es la función de error complementaria , erfc comúnmente denotado (z) , es una función entera definido por ERFC ( z ) = 1 - erf ( z ) ( 1 ) = 2 / ( sqrt ( pi) ) ^ int_z inftye ^ ( - t ^ 2 ) dt . ( 2 ) Se implementa en el lenguaje como Wolfram ERFC [ z ] . Tenga en cuenta que algunos autores ( por ejemplo, Whittaker y Watson , 1990, pág . 341 ) definen ERFC ( z ) sin el factor principal de 2 / sqrt ( pi) . Para z > 0 , erfc (z ) = ( Gamma ( 1/2 , z ^ 2 ) ) / ( sqrt (pi) ) , ( 3 ) donde Gamma (a, x ) es la función gamma incompleta . El derivado es dada por d / ( dz ) ERFC ( z ) = - ( 2e ^ ( - z ^ 2 ) ) / ( sqrt ( pi) ) , ( 4 ) y la integral indefinida por interFC ( z ) dz = zerfc ( z ) - ( e ^ ( - z ^ 2 ) ) / ( sqrt ( pi) ) + C . ( 5 ) Tiene los valores especiales erfc ( -infty ) = 2 ( 6 ) erfc ( 0 ) = 1 ( 7 ) ERFC ( infty ) = 0 . ( 8 ) Satisface la identidad erfc (-x ) = 2 - erfc (x).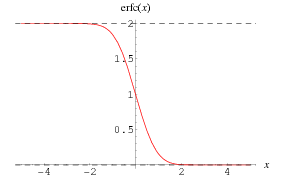
Aplicaciones de la función error.
Función error de Gauss Una de las funciones matemáticas que, auncllie
elemental, todavía no suele venir predefinida en las calculadoras de bolsillo, es
la función error de Gauss, erf(x), la cual aparece en muchos desarrollos de la
Tern~odinán~ica estadística, la Transmisión de calor y la Metrología
experimental. Esta función está basada en la distribución de probabilidad
normal, que es a la que tienden todas las funciones de distribución de
probabilidad al aumentar el número de casos que se consideran. A modo de
ejemplo, considérese un tirador que dispara a un blanco puntual.1. Termodinámica : Distribución de la energía entre las moléculas
La energía de una partícula de masa m que se mueve
en una región unidimensional de anchura a no puede
tener cualquier valor. Cuando resolvemos la ecuación
de Schrödinger para una partícula que se mueve en
cubo de anchura a obtenemos los niveles de energía
que puede ocupar dicha partícula.
siendo n x , n y , y n z números enteros positivos.
Cuando a es grande, como ocurre para las partículas de un gas encerrado en
un recipiente, los niveles de energía están muy juntos. Nuestra tarea ahora es
la de calcular el número de niveles de energía comprendidos en el intervalo
entre E y E+dE.
2. Transferencia de calor: La Ley de Distribución de las Velocidades Moleculares
En un gas ideal encerrado en un recipiente, el movimiento de las moléculas es
completamente al azar, es decir, todas las direcciones del espacio son
igualmente probables. Pero no es posible que todas las velocidades v de las
moléculas sean igualmente probables ya que hay una relación lineal entre el
valor medio cuadrático de la velocidad y la temperatura absoluta del gas ideal.
La energía de una partícula de masa m que se mueve en una región
unidimensional de anchura a no puede tener cualquier valor. Cuando
resolvemos la ecuación de Schrödinger para una partícula que se mueve en
cubo de anchura a obtenemos los niveles de energía que puede ocupar dicha
partícula.
De transmisión de calor basado en el contacto directo entre los cuerpos, sin
intercambio de materia, por el que el calor fluye desde un cuerpo de mayor
temperatura a otro de menor temperatura que está en contacto con el primero.
La propiedad física de los materiales que determina su capacidad para
conducir el calor es la conductividad térmica. La propiedad inversa de la
conductividad térmica es la resistividad térmica, que es la capacidad de los
materiales para oponerse al paso del calor.
La transmisión de calor por conducción, entre dos cuerpos o entre diferentes
partes de un cuerpo, es el intercambio de energía interna, que es una
combinación de la energía cinética y energía potencial de sus partículas
microscópicas: moléculas, átomos y electrones. La conductividad térmica de la
materia depende de su estructura microscópica: en un fluido se debe
principalmente a colisiones aleatorias de las moléculas; en un sólido depende
del intercambio de electrones libres (principalmente en metales) o de los modos
de vibración de sus partículas microscópicas (dominante en los materiales no
metálicos).
Para el caso simplificado de flujo de calor estacionario en una sola dirección, el
calor transmitido es proporcional al área perpendicular al flujo de calor, a la
conductividad del material y a la diferencia de temperatura, y es inversamente
proporcional al espesor
La conducción de calor o transmisión de calor por conducción es un proceso
X es el espesor del material
Podemos hallar la energía del gas ideal mediante
Dividiendo entre N, número de moléculas, obtenemos la energía media de las
moléculas es 3kT/2
Por tanto, la energía de las moléculas de un gas ideal monoatómico es
proporcional a la temperatura absoluta del gas. Históricamente esta ecuación
fue introducida en el siglo XIX mucho antes del desarrollo de la Mecánica
Estadística, en conexión con la teoría cinética de los gases.
El número N de moléculas es igual al número de moles m por el número de
Avogadro N 0 =6.0225 10 23 mol -1 . El producto del número de Avogadro por la
constante de Boltzmann k=1.38 10 -23 J/K nos da la constante R=8.3143 J/(K
mol) de los gases ideales.
Los datos experimentales están de acuerdo con la teoría, lo que confirma la
aplicabilidad de la estadística de Maxwell-Boltzmann. Por ejemplo, una
reacción determinada ocurre solamente si las moléculas tienen cierta energía
igual o mayor que E 0 . La velocidad de la reacción a una temperatura dada
depende entonces, del número de moléculas que tienen una energía mayor o
igual que E 0 .3. Economía: En estadística, se dice que hay endogeneidad cuando hay una correlación
entre el parámetro o variable y el término de error. La endogeneidad puede
surgir como resultado de un error de
medición, autorregresión con autocorrelación de errores, simultaneidad y
variables omitidas. En términos generales, un lazo de causalidad entre los
independientes y las variables dependientes de un modelo conduce a la
endogeneidad.
Por ejemplo, en un simple modelo de oferta y demanda, al momento de
predecir la cantidad demandada en equilibrio, el precio es endógeno porque los
productores cambian su precio en función de la demanda y los consumidores
cambian su demanda en respuesta a los precios. En este caso, se dice que la
variable de precio tiene endogeneidad total una vez conocidas las curvas de
demanda y oferta. En contraste, un cambio en el consumo gustos o
preferencias sería un cambio exógeno en la curva de demanda.
Aplicación de la Ecuación de Ricatti en Ingeniería Química
Al ser una forma particular de la ecuación de Bernoulli,su principal aplicación es en la hidrodinámica, es decir te permite relacionar,variables como velocidad, presion, densidad en un fluido contenido por una tuberia con cambios de nivel y de seccion transversal.
Aplicaciones prácticas de esta ecuación se la encuentra
- Tubo de Venturi : Estos tubos sirven para medir la diferencia de presión entre el fluido que pasa a baja velocidad por una entrada amplia comparada con el fluido que pasa por un orificio de menor diámetro a alta velocidad.
- Carburador de automovil: En un carburador de automóvil, la presión del aire que pasa a través del cuerpo del carburador, disminuye cuando pasa por un estrangulamiento. Al disminuir la presión, la gasolina fluye, se vaporiza y se mezcla con la corriente de aire.
- Industria de envasado de perfumes: Específicamente en su atomizador ya que todos los atomizadores basan su funcionamiento en el Principio de Bernoulli.
- Tuberías: Es su uso más conocido debido a que La ecuación de Bernoulli también nos dice que si reducimos el área transversal de una tubería para que aumente la velocidad del fluido, se reducirá la presión. así mismo, es el más estudiado



martes, 19 de julio de 2016
Deber 19/07/2016
Al subir el archivo a SCRIBD se desordena, adjunto un link de descarga del archivo para mejor visualización :) https://drive.google.com/open?id=0B7B88lrU5Gx9bEF0WVNwUzJ4ek0
viernes, 10 de junio de 2016
lunes, 30 de mayo de 2016
Ley de los gases Ideales
Qué son gases ideales?
Un gas ideal es un gas teórico compuesto de un conjunto de partículas puntuales con desplazamiento aleatorio que no interactúan entre sí. El concepto de gas ideal es útil porque el mismo se comporta según la ley de los gases ideales, una ecuación de estado simplificada, y que puede ser analizada mediante la mecánica estadística.
Tipos de gases ideales
Existen tres clases básicas de gas ideal:
- El clásico o gas ideal de Maxwell-Boltzmann
- El gas ideal cuántico de Bose, compuesto de bosones
- El gas ideal cuántico de Fermi, compuesto de fermiones
Ley de Boyle
La Ley de Boyle-Mariotte (o Ley de Boyle), formulada por Robert Boyle y Edme Mariotte, es una de las leyes de los gases ideales que relaciona el volumen y la presión de una cierta cantidad de gas mantenida a temperatura constante. La ley dice que el volumen es inversamente proporcional a la presión: 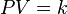
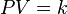
donde  es constante si la temperatura y la masa del gas permanecen constantes.
es constante si la temperatura y la masa del gas permanecen constantes.
 es constante si la temperatura y la masa del gas permanecen constantes.
es constante si la temperatura y la masa del gas permanecen constantes.
Cuando aumenta la presión, el volumen disminuye, mientras que si la presión disminuye el volumen aumenta. El valor exacto de la constante k no es necesario conocerlo para poder hacer uso de la Ley; si consideramos las dos situaciones de la figura, manteniendo constante la cantidad de gas y la temperatura, deberá cumplirse la relación
Ley de Charles
Si la cantidad de gas y la presión permanecen constantes, es razonable suponer que el volumen aumente al aumentar la temperatura. Un aumento de temperatura implica un aumento de la energía cinética media de las partículas, por tanto, un aumento de su velocidad y de la frecuencia e intensidad de los choques de éstas con las paredes. Si la pared es elástica (por ejemplo, un globo) o se puede desplazar (por ejemplo, un embolo) y la presión exterior (que iguala a la interior) permanece constante, entonces planteamos que el volumen del gas, V, debe ser proporcional a su temperatura, T (V = K · T , para P y N constantes).
Ley de Gay-Lussac
Si la cantidad de gas y el volumen permanecen constantes, es lógico suponer que la presión aumente al aumentar la temperatura. Como hemos comentado, un aumento de temperatura implica un aumento de la velocidad de las partículas y, en consecuencia, de la frecuencia e intensidad de los choques de ellas con las paredes. Matemáticamente expresamos la segunda ley de Gay-Lussac ley diciendo que la presión, P, debe ser proporcional a la temperatura (P = k · T , para V y N constantes)
Todas ellas se condensan en la siguiente fórmula que es aplicable para una misma cantidad de gas:
Por esta razón y para n moles siendo las condiciones de presión y temperatura cualesquiera podemos poner que:
P1 · V1 / T1 = P2 · V2 / T2
PV = nRT
|
- P es la presión
- V es el volumen
- T es la temperatura absoluta (en grados Kelvin)
- R Pertenece a un valor constante. Conocida como constante ideal de los gases
Esta es conocida como la ley general de los gases.
domingo, 29 de mayo de 2016
Fuerza Centrífuga Y centrípeta. Aplicación de tercera derivada
Fuerza Centrípeta
Proveniente del vocablo en latín Centrípetus refiere a lo que se desplaza rumbo al centro o a lo que produce atracción hacia la ubicación de él
 |
| Atracción hacia el centro de la curva |
os objetos con movimiento rectilíneo uniforme tienen una velocidad constante; pero un objeto que se mueva sobre una trayectoria circular con rapidez constante experimenta continuamente un cambio en la dirección de su movimiento, esto es, en la dirección de la velocidad. Puesto que la velocidad cambia, existe una aceleración. La magnitud de este cambio de dirección de la velocidad por unidad de tiempo es la aceleración centrípeta, representada por un vector dirigido hacia el centro de la circunferencia dado por
Donde:
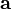 es la aceleración centrípeta.
es la aceleración centrípeta. es el módulo de la velocidad.
es el módulo de la velocidad. es el radio de la trayectoria circular (en general, el radio de curvatura).
es el radio de la trayectoria circular (en general, el radio de curvatura).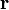 el vector de posición.
el vector de posición.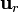 el versor radial.
el versor radial. la velocidad angular.
la velocidad angular.- Según la segunda ley de Newton, para que se produzca una aceleración debe actuar una fuerza en la dirección de esa aceleración. Así, si consideramos una partícula de masa
 en movimiento circular uniforme, estará sometida a una fuerza centrípeta dada por:
en movimiento circular uniforme, estará sometida a una fuerza centrípeta dada por:
Ejemplos en la vida cotidiana.
- Atracción del Sol a la tierra y demás planetas. Debido a la gran masa del sol este ejerce un fuerza gravitacional (centrípeta) sobre la tierra que la obliga a describir una trayectoria elíptica
- Rotación de la tierra con respecto al sol. Así mismo como la tierra es atraída al sol por su considerable mas, la fuerza centrífuga evita que el planeta choque con la estrella
- La lavadora al lavar la ropa. Cuando el tambor de la lavadora internamente gira a alta velocidad ocurre que la ropa queda pegada a la pared del tambor, esta acción producida por la fuerza centrífuga
- Al dar vueltas con agarrado a un eje vertical ( que podría ser otra persona) el cuerpo va a sentir que está siendo atraído hacia atrás, sin embargo al soltarse se genera una trayectoria tangencial
2. Un objeto que se hace girar amarrado a una cuerda. Al hacerlo con la suficiente fuerza, el objeto va a estirar la cuerda de tal forma que describe una trayectoria circular, sin embargo... El cuerpo no puede seguir su trayectoria tangencial como debería ya que la cuerda está ejerciendo una fuerza centrípeta sobre el.

3. En un rizo de una montaña rusa. Al momento en el que los pasajeros de la montaña rusa están de cabeza van a sentir que son impulsados hacia el centro del rizo, debido a la sumatoria de pesos entre el carro y el peso de la persona, sin embargo, los cinturones de seguridad mantienen al pasajero en su sitio
Fuerza centrífuga
La fuerza centrifuga esta basada en un eje de referencia con eje giratorio, respecto del cual, el objeto que gira a su alrededor crea una fuerza no visible hacia afuera, se supone en el estudio, que dicha partícula esta atada al eje, creando un patrón de revolución paralelo respecto de donde se origina la fuerza.
Perteneciente a la mecánica newtoniana, La Fuerza Centrifuga y si opuesta La Fuerza centrípeta son magnitudes a las que no se le aprecia la sensación desde el punto de vista de un espectador. La fuerza centrifuga, desplaza al cuerpo por inercia hacia afuera del eje ya que la gravedad y el peso permiten que ese Fenómeno ocurra, sin embargo, quien ve el desde afuera del eje el comportamiento del objeto, no percibirá la atracción de un vacío inexistente que hala al cuerpo fuera de su eje.

Ejemplos en la vida cotidiana.
Aplicaciones de la tercera derivada.
La tercera derivada permite indicar en caso de que la función tenga máximos o mínimos, si el valor de la incógnita es mayor que 0, el valor es un mínimo. Si en cambio, es menor que 0, el valor es un máximo.Ahora, en general, en física muchos fenómenos se pueden describir por medio de una función escalar, denominada potencial que se extiende sobre alguna región en particular (por ejemplo el potencial gravitatorio o eléctrico) con la cual se puede asociar energía potencial a una partícula en dicha región.
La tercera derivada de la energía potencial (segunda de la fuerza) nos indicaría sobre las regiones en las cuales la fuerza toma valores extremales (máximos o mínimos).
Se podría saber en que regiones, afectadas por una distribución de cargas, la fuerza eléctrica sobre una carga de prueba será máxima o mínima (localmente).
Suscribirse a:
Comentarios (Atom)





