Taller de matemáticas

16/08/2016

Taller Matemáticas 3 by Stephanie Mosquera on Scribd

Función Error(erf) y Función Error Complementario(erfc)

Función Error

La función error, denotada como erf ( x) , es una función trascendental que aparece en probabilidad, estadística, y en la solución de ecuaciones diferenciales parciales. También se le conoce como función error de Gauss. 

En matemáticas, la función error  es una función especial (no elemental) que se utiliza en el campo de la probabilidad, la estadística y las ecuaciones diferenciales parciales. La función queda definida por la expresión:

${\displaystyle \operatorname {erf} (x)={\frac {2}{\sqrt {\pi }}}\int _{0}^{x}e^{-t^{2}}\,\mathrm {d} t}$

La función error complementaria, llamada erfc, se define a partir de la función error:

${\displaystyle {\mbox{erfc}}(x)=1-{\mbox{erf}}(x)={\frac {2}{\sqrt {\pi }}}\int _{x}^{\infty }e^{-t^{2}}\,\mathrm {d} t}$

Grafica de la función error

Función Error Complementaria 

Erfc es la función de error complementaria , erfc comúnmente denotado (z) , es una función entera definido por

ERFC ( z ) = 1 - erf ( z )
( 1 )
= 2 / ( sqrt ( pi) ) ^ int_z inftye ^ ( - t ^ 2 ) dt .
( 2 )
Se implementa en el lenguaje como Wolfram ERFC [ z ] .

Tenga en cuenta que algunos autores ( por ejemplo, Whittaker y Watson , 1990, pág . 341 ) definen ERFC ( z ) sin el factor principal de 2 / sqrt ( pi) .

Para z > 0 ,

 erfc (z ) = ( Gamma ( 1/2 , z ^ 2 ) ) / ( sqrt (pi) ) ,
( 3 )
donde Gamma (a, x ) es la función gamma incompleta .

El derivado es dada por

 d / ( dz ) ERFC ( z ) = - ( 2e ^ ( - z ^ 2 ) ) / ( sqrt ( pi) ) ,
( 4 )
y la integral indefinida por

 interFC ( z ) dz = zerfc ( z ) - ( e ^ ( - z ^ 2 ) ) / ( sqrt ( pi) ) + C .
( 5 )
Tiene los valores especiales

erfc ( -infty ) = 2
( 6 )
erfc ( 0 ) = 1
( 7 )
ERFC ( infty ) = 0 .
( 8 )
Satisface la identidad

 erfc (-x ) = 2 - erfc (x).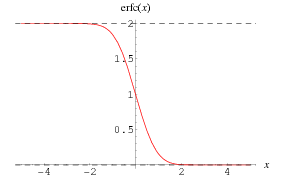

Aplicaciones de la función error.

Función error de Gauss Una de las funciones matemáticas que, auncllie
elemental, todavía no suele venir predefinida en las calculadoras de bolsillo, es
la función error de Gauss, erf(x), la cual aparece en muchos desarrollos de la
Tern~odinán~ica estadística, la Transmisión de calor y la Metrología
experimental. Esta función está basada en la distribución de probabilidad
normal, que es a la que tienden todas las funciones de distribución de
probabilidad al aumentar el número de casos que se consideran. A modo de
ejemplo, considérese un tirador que dispara a un blanco puntual.

1. Termodinámica : Distribución de la energía entre las moléculas
La energía de una partícula de masa m que se mueve
en una región unidimensional de anchura a no puede
tener cualquier valor. Cuando resolvemos la ecuación
de Schrödinger para una partícula que se mueve en
cubo de anchura a obtenemos los niveles de energía
que puede ocupar dicha partícula.
siendo n x , n y , y n z  números enteros positivos.
Cuando a es grande, como ocurre para las partículas de un gas encerrado en
un recipiente, los niveles de energía están muy juntos. Nuestra tarea ahora es
la de calcular el número de niveles de energía comprendidos en el intervalo
entre E y E+dE.
 


2. Transferencia de calor: La Ley de Distribución de las Velocidades Moleculares

En un gas ideal encerrado en un recipiente, el movimiento de las moléculas es
completamente al azar, es decir, todas las direcciones del espacio son
igualmente probables. Pero no es posible que todas las velocidades v de las
moléculas sean igualmente probables ya que hay una relación lineal entre el
valor medio cuadrático de la velocidad y la temperatura absoluta del gas ideal.
La energía de una partícula de masa m que se mueve en una región
unidimensional de anchura a no puede tener cualquier valor. Cuando
resolvemos la ecuación de Schrödinger para una partícula que se mueve en
cubo de anchura a obtenemos los niveles de energía que puede ocupar dicha
partícula.
 De transmisión de calor basado en el contacto directo entre los cuerpos, sin
intercambio de materia, por el que el calor fluye desde un cuerpo de mayor
temperatura a otro de menor temperatura que está en contacto con el primero.
La propiedad física de los materiales que determina su capacidad para
conducir el calor es la conductividad térmica. La propiedad inversa de la
conductividad térmica es la resistividad térmica, que es la capacidad de los
materiales para oponerse al paso del calor.
La transmisión de calor por conducción, entre dos cuerpos o entre diferentes
partes de un cuerpo, es el intercambio de energía interna, que es una
combinación de la energía cinética y energía potencial de sus partículas
microscópicas: moléculas, átomos y electrones. La conductividad térmica de la
materia depende de su estructura microscópica: en un fluido se debe
principalmente a colisiones aleatorias de las moléculas; en un sólido depende
del intercambio de electrones libres (principalmente en metales) o de los modos
de vibración de sus partículas microscópicas (dominante en los materiales no
metálicos).
Para el caso simplificado de flujo de calor estacionario en una sola dirección, el
calor transmitido es proporcional al área perpendicular al flujo de calor, a la
conductividad del material y a la diferencia de temperatura, y es inversamente
proporcional al espesor
La conducción de calor o transmisión de calor por conducción es un proceso
X es el espesor del material


Podemos hallar la energía del gas ideal mediante
Dividiendo entre N, número de moléculas, obtenemos la energía media de las
moléculas es 3kT/2
Por tanto, la energía de las moléculas de un gas ideal monoatómico es
proporcional a la temperatura absoluta del gas. Históricamente esta ecuación
fue introducida en el siglo XIX mucho antes del desarrollo de la Mecánica
Estadística, en conexión con la teoría cinética de los gases.
El número N de moléculas es igual al número de moles m por el número de
Avogadro N 0 =6.0225 10 23  mol -1 . El producto del número de Avogadro por la
constante de Boltzmann k=1.38 10 -23  J/K nos da la constante R=8.3143 J/(K
mol) de los gases ideales.
Los datos experimentales están de acuerdo con la teoría, lo que confirma la
aplicabilidad de la estadística de Maxwell-Boltzmann. Por ejemplo, una
reacción determinada ocurre solamente si las moléculas tienen cierta energía
igual o mayor que E 0 . La velocidad de la reacción a una temperatura dada
depende entonces, del número de moléculas que tienen una energía mayor o
igual que E 0 .


3. Economía:  En estadística, se dice que hay endogeneidad cuando hay una correlación
entre el parámetro o variable y el término de error. La endogeneidad puede
surgir como resultado de un error de
medición, autorregresión con autocorrelación de errores, simultaneidad y
variables omitidas. En términos generales, un lazo de causalidad entre los
independientes y las variables dependientes de un modelo conduce a la
endogeneidad.
Por ejemplo, en un simple modelo de oferta y demanda, al momento de
predecir la cantidad demandada en equilibrio, el precio es endógeno porque los
productores cambian su precio en función de la demanda y los consumidores
cambian su demanda en respuesta a los precios. En este caso, se dice que la
variable de precio tiene endogeneidad total una vez conocidas las curvas de
demanda y oferta. En contraste, un cambio en el consumo gustos o
preferencias sería un cambio exógeno en la curva de demanda.

Aplicación de la Ecuación de Ricatti en Ingeniería Química

Al ser  una forma particular de la ecuación de Bernoulli,su principal aplicación es en la hidrodinámica, es decir te permite relacionar,variables como  velocidad, presion, densidad en un fluido contenido por una tuberia con cambios de nivel y de seccion transversal. 
Aplicaciones prácticas de esta ecuación se la encuentra 

• Tubo de Venturi : Estos tubos sirven para medir la diferencia de presión entre el fluido que pasa a baja velocidad por una entrada amplia comparada con el fluido que pasa por un orificio de menor diámetro a alta velocidad.
• Carburador de automovil: En un carburador de automóvil, la presión del aire que pasa a través del cuerpo del carburador, disminuye cuando pasa por un estrangulamiento. Al disminuir la presión, la gasolina fluye, se vaporiza y se mezcla con la corriente de aire.
• Industria de envasado de perfumes: Específicamente en su atomizador ya que todos los atomizadores basan su funcionamiento en el Principio de Bernoulli.
• Tuberías: Es su uso más conocido debido a que La ecuación de Bernoulli también nos dice que si reducimos el área transversal de una tubería para que aumente la velocidad del fluido, se reducirá la presión. así mismo, es el más estudiado